深度学习基本原理

• GitHub: https://github.com/Humoonruc/deep-learning-notes
• Web Pages: https://humoonruc.github.io/deep-learning-notes/

简介

深度学习在结构上是一种链式几何变换，本质上是一种高度复杂的非线性回归分析方法，应用重点在于预测而非解释¹。

选择深度模型而非浅层模型²，本质上是牺牲一些可解释性来换取更好的预测性。所以，深度学习天然与更实用主义的产业界更亲和，而与更理论化的学术界更疏远。

易混淆的相关概念

1 人工智能（AI）

在一定程度上，Artificial Intelligence 是自动化的另一种说法。

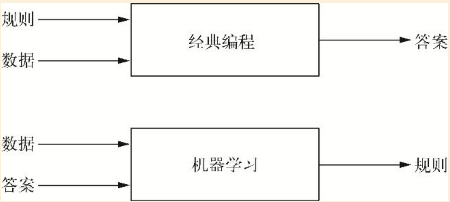
2 机器学习

• 避免硬编码，从已有的数据中寻找映射的规则（回归分析也是一种机器学习），然后使用这种规则用于推断和预测。
• 当然，模型的类型和基本结构是由人工进行事先约束的，机器学习主要是一个参数优化的过程。
• 在神经网络之外，其他机器学习方法包括逻辑回归(logistic regression)、决策树等。

• 与经典的统计学不同，机器学习倾向于处理大型、复杂的数据集。
• 机器学习主要是面向工程的，因此数学理论较少，往往通过经验而非理论来推进。
• 处理非感知数据的浅层机器学习算法中，最流行的技术是梯度提升机，这是一种基于集成弱测试模型（通常是决策树）的机器学习技术。

3 神经网络（Neural Networks）

• 神经元（多个接收电信号的树突和一个输出电信号的轴突）是一个形象的比喻。这里指由一个或多个参数输入产生输出的结构。w 和 b 是参数或权重 weights，前者称为 kernel，后者称为 bias

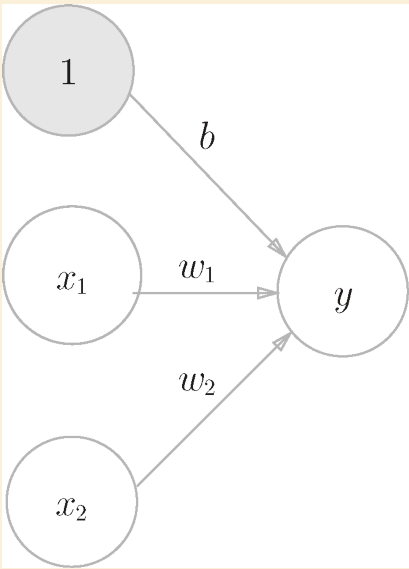
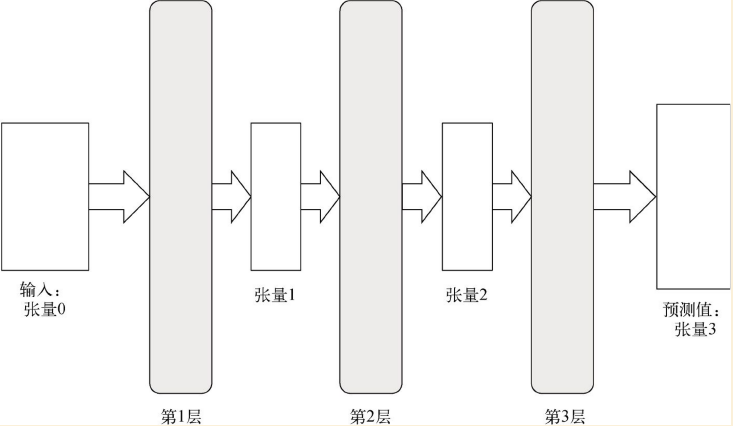
• 多个、多层神经元联合工作，就构成了神经网络。中间层也称隐藏层。

• 结构示意图：从输入张量X到输出张量Y，通过连续的数学运算层来转换数据的表示。

  • 转换数据的表示是神经网络的核心问题。
  • 神经网络主要是一个历史概念，更准确的名称应该是分层表述学习或链式几何变换。

• 神经网络是用于解开复杂的高维数据流形的数学机器

  • 一个形象的比喻：两张不同颜色的纸，揉在一起，每张纸都是分类问题中的一类数据。神经网络就是要找到一种能够将纸团展平的变换，从而使两个类别再次完全分离。
  • 多层神经网络将一个复杂的几何变换逐步分解为一长串基本变换，几乎就是人类展开纸球时遵循的策略。

4 深度学习

深度学习指层数很多（前沿模型的层数甚至高达上千层）的神经网络模型，是转换数据表示的多阶段方法。

近十年推动深度学习快速普及的因素

像任何革命一样，深度学习的革命是大量因素积累的产物。

硬件

支持并行计算的 GPU³ 集群。业界前沿正在开发专门用于深度学习计算的 TPU（张量处理单元）。

大数据

互联网和移动互联网的普及，使拥有标记的数据（即{值:标签}对）指数级增长。

算法改进

更好的激活函数（如 ReLU，线性整流函数）

更好的权重初始化方案

更好的参数优化方案（如 adam，RMSProp）

批次标准化、残差连接、深度可分卷积……

软件框架和 API

CUDA，TensorFlow，Keras……

未来

深度学习可能会被过度炒作几年，但从长远来看，它仍是一场将改变我们的经济和生活的重大革命。

JavaScript 深度学习的优缺点

优势

• 可以运行在浏览器中，简化部署
• 可以利用浏览器的 WebGL 接口，调用显卡 GPU 的并行计算功能加速模型训练
• JavaScript 生态拥有最强大、最成熟的可视化方案
• V8 引擎的强大性能支持，比 Python 快

缺点

浏览器环境性能有限，商业前沿级别的复杂任务（如机器翻译）所需的超大规模模型的训练必须使用服务器集群。

TensorFlow.js

TensorFlow.js | TensorFlow中文官网

tensorflow/tfjs-examples: Examples built with TensorFlow.js (github.com)

• tensor flow，张量流，对多层神经网络很形象的提炼

• TensorFLow，Google 开发的深度学习低阶 API

• Keras，深度学习高阶API，提供了常用的神经网络层类型

• TensorFlow.js

  • Google 深度学习团队开发的 JavaScript 第三方库
  • 同时具有低阶和高阶 API，兼容 TensorFlow 和 Keras
  • 支持导入和导出 TensorFlow 和 Keras 的深度学习模型

通用工作流程

1. 定义问题，收集数据
2. 确定衡量模型的统计量
3. 定义训练集、验证集、测试集
4. 数据张量化和标准化
5. 训练第一个模型，观察结果是否能超越普通常识基准
6. 调整超参数、添加正则化项，逐步优化模型结构
7. 注意验证集的过拟合

三种层结构

dense 层

卷积层

递归层

建立模型：forward pass

forward pass: 将 $X$$X$ 输入模型获得 $\hat{Y}$$\hat{Y}$ 的过程

感知机（Perceptron）

• 感知机模拟单个神经元，将输入的权重 (w) 和偏置（b）设定为参数。
• 使用感知机可以表示与门和或门等逻辑电路。
• 异或门无法通过单层感知机来表示，但双层感知机就可以表示异或门。
• 单层感知机只能表示线性空间，而多层感知机（multi-layer perceptron, MLP）可以表示非线性空间。加深层级一般可以提升模型的性能。
• 多层感知机（在理论上）可以表示计算机。

激活函数 activation function⁴

激活函数 h() 用 sigmoid, ReLU 等函数对输入信号的线性组合进行改造，然后发给下一个神经元。

sigmoid 函数（它的形状近似阶跃分段函数，但却是平滑可导的）：

ReLU（Rectified Linear Unit, 线性整流）函数：

tanh 函数：

sigmoid 函数的缺点在于，当 x 值远离 0 时，导数几乎为0，使得梯度下降难以进行，这被称为“梯度消失”。而 ReLU 函数在 x>0 时的导数恒为 1，分析性质十分良好，故 ReLU 激活函数一般被作为隐藏层的默认激活函数。而输出层的激活函数，一般会根据问题的需要来选择（二分类问题用 sigmoid，多分类问题用 softmax）。

激活函数不能用线性函数，否则多层神经网络的输出还是输入的线性组合，就没必要用多层了。

多层感知机+激活函数就构成了神经网络。

神经网络本质上就是非线性函数的复合，每一层都是一个非线性函数，最后得到一个超级复杂的复合函数。

类型分割线

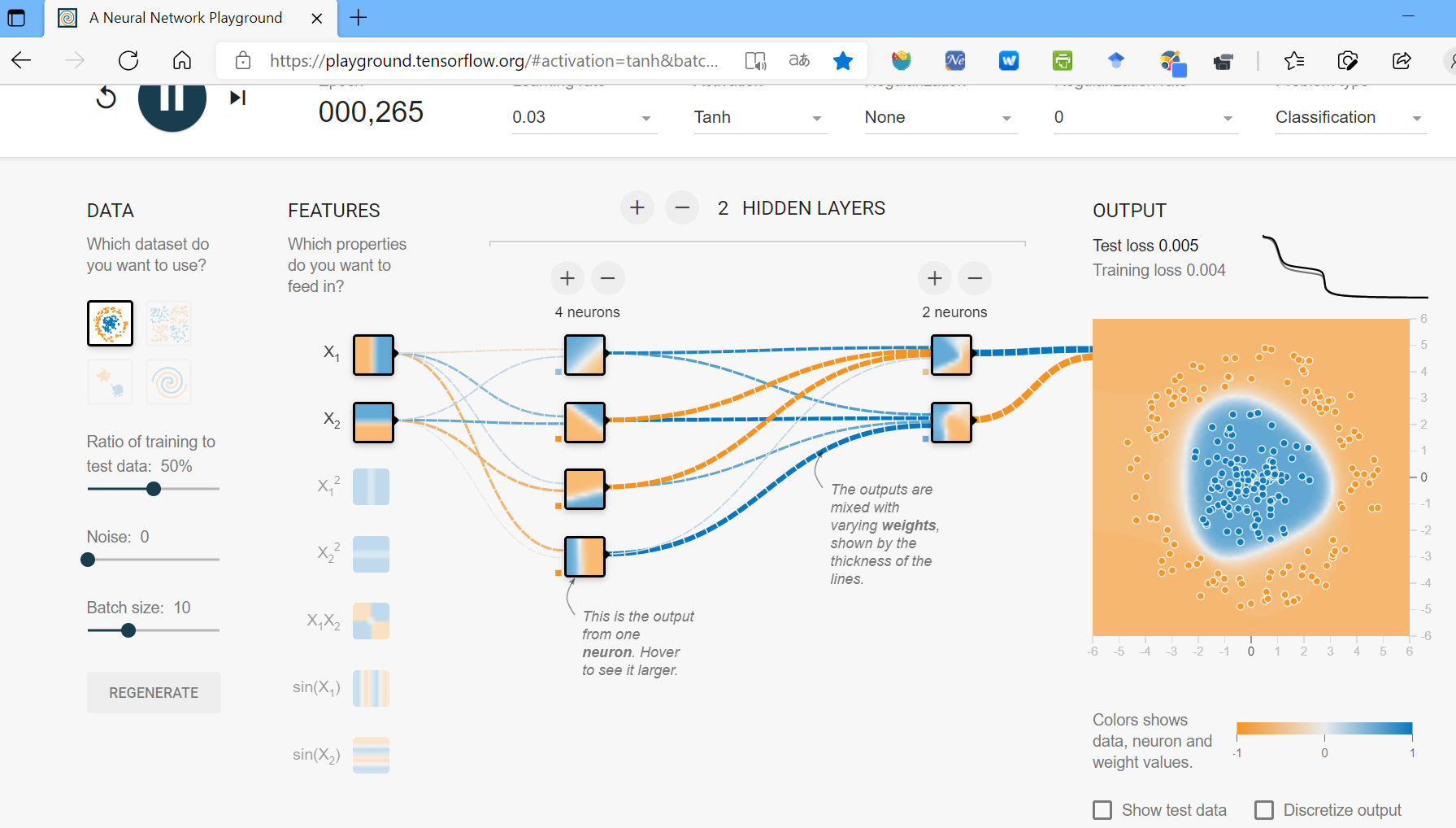
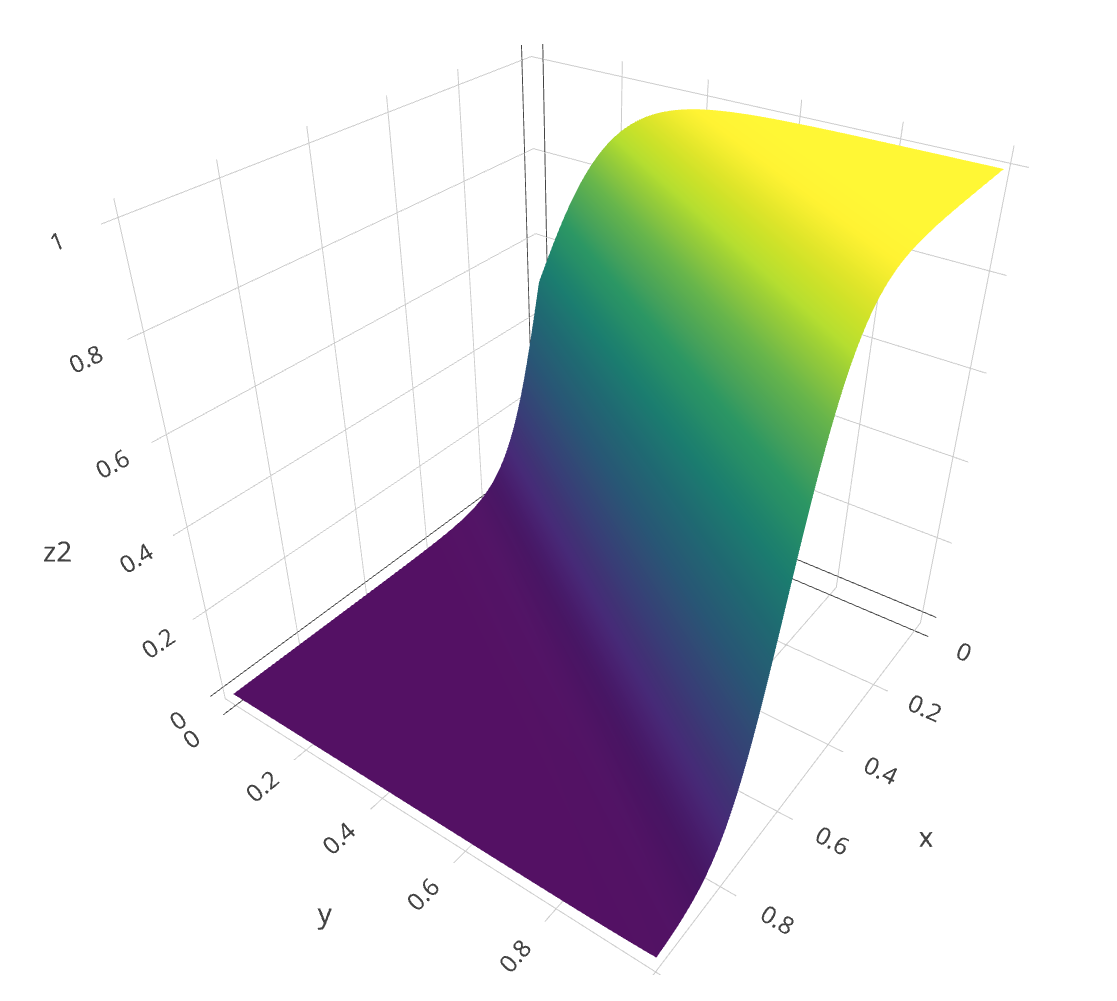
一元线性函数经过 sigmoid 函数的转换，在x-y坐标系中会显示为 S 型曲线；二元线性函数在三维直角坐标系中表现为二维平面，被 sigmoid 函数转换后会成为 S 型曲面。

曲面上 z=0.5 的点，投影到 x-y 平面上，是一条直线，称为类型分割线。该线的两边，z 值分别大于和小于0.5

但如果样本中 z 值大于和小于 0.5 的点无法用一条直线分开，便称之为线性不可分问题。此时，必须增加神经网络模型的层数，扭曲 sigmoid 曲面为更加复杂的形状，从而类型分割线也会扭曲为曲线，才能较好地拟合数据。

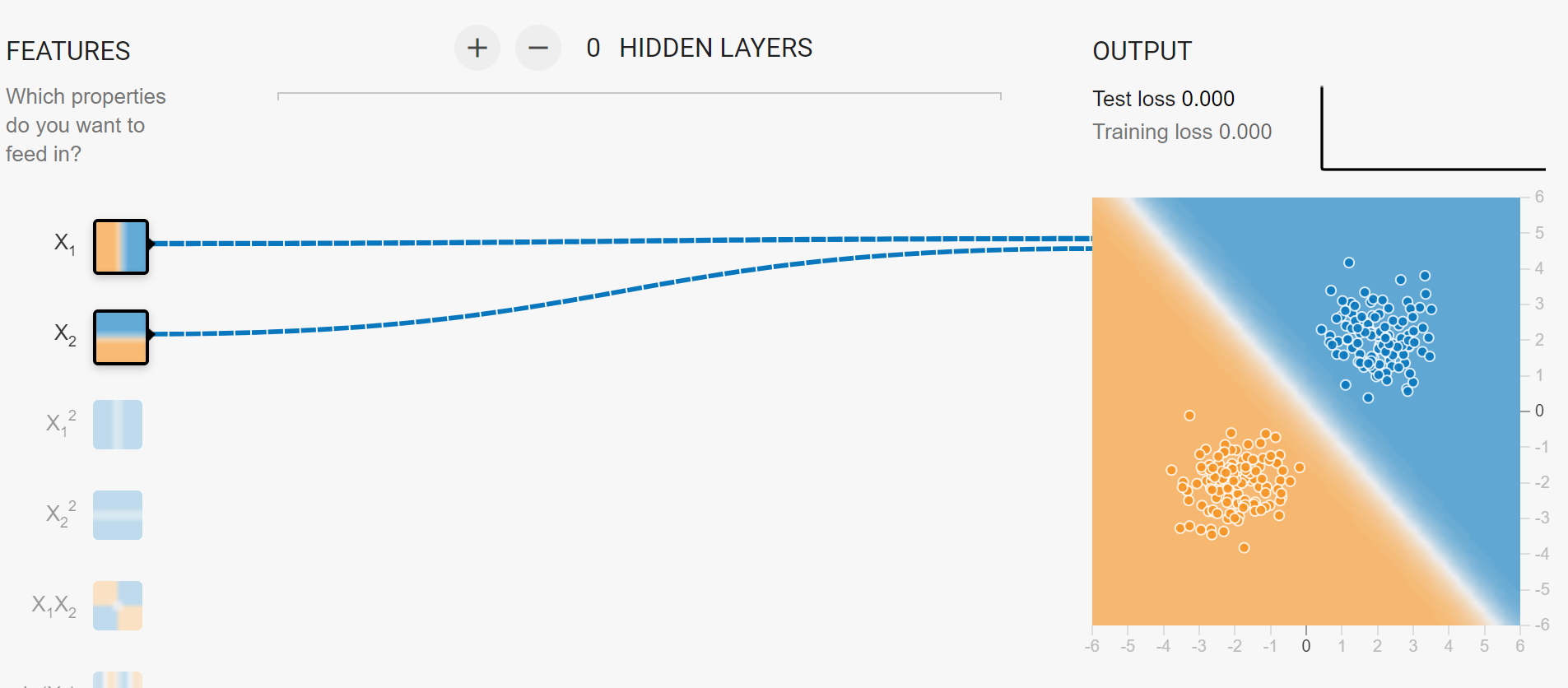
如图，单层两个神经元，即可处理线性可分的样本。

线性不可分的样本：

用两层神经网络（也被称为在输入层、输出层之外含有一个隐藏层），隐藏层包含 3 个（或以上）神经元，即可处理圆环型分布的样本。

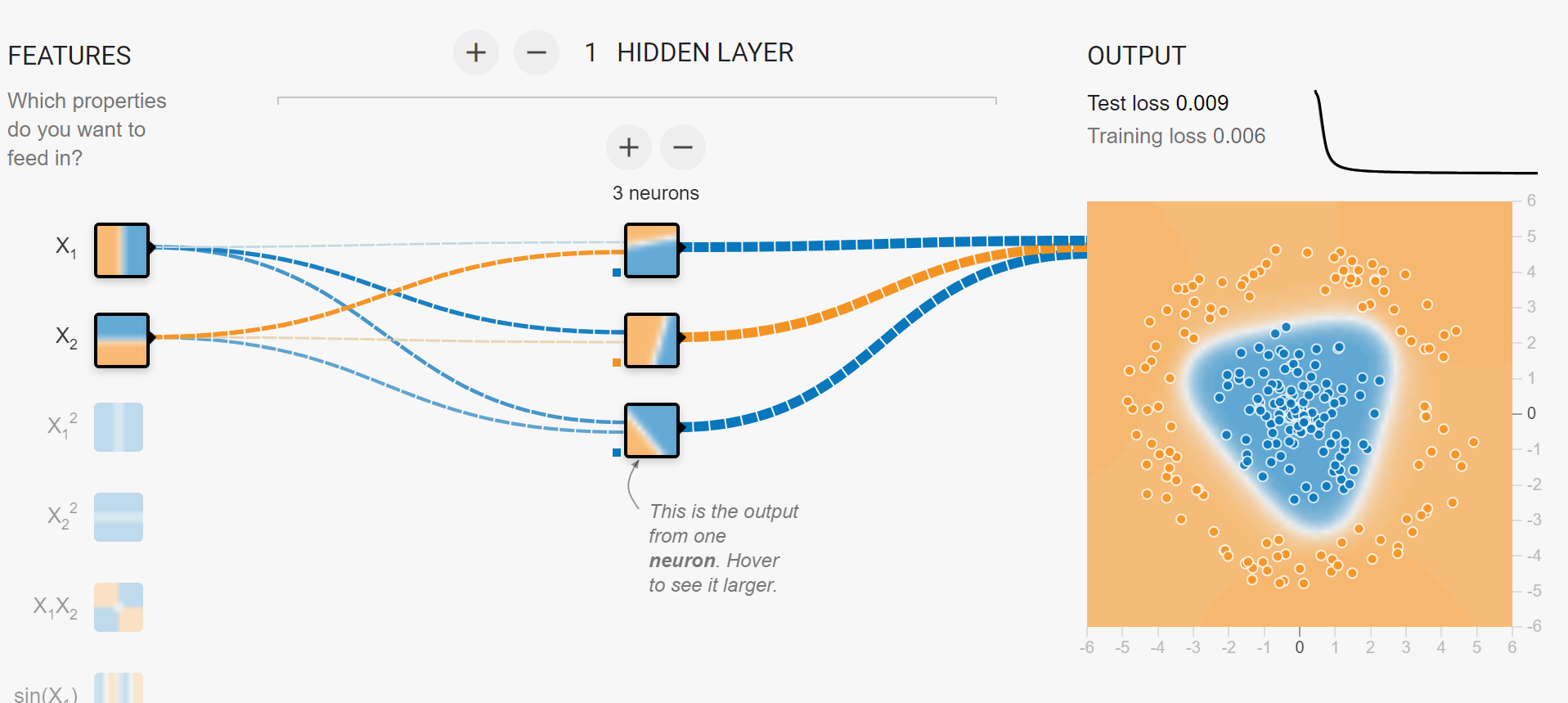
隐藏层 3 个（或以上）神经元可以分离花瓣型分布的样本，但拟合效果不够好。4 个以上的神经元才能较好地处理。

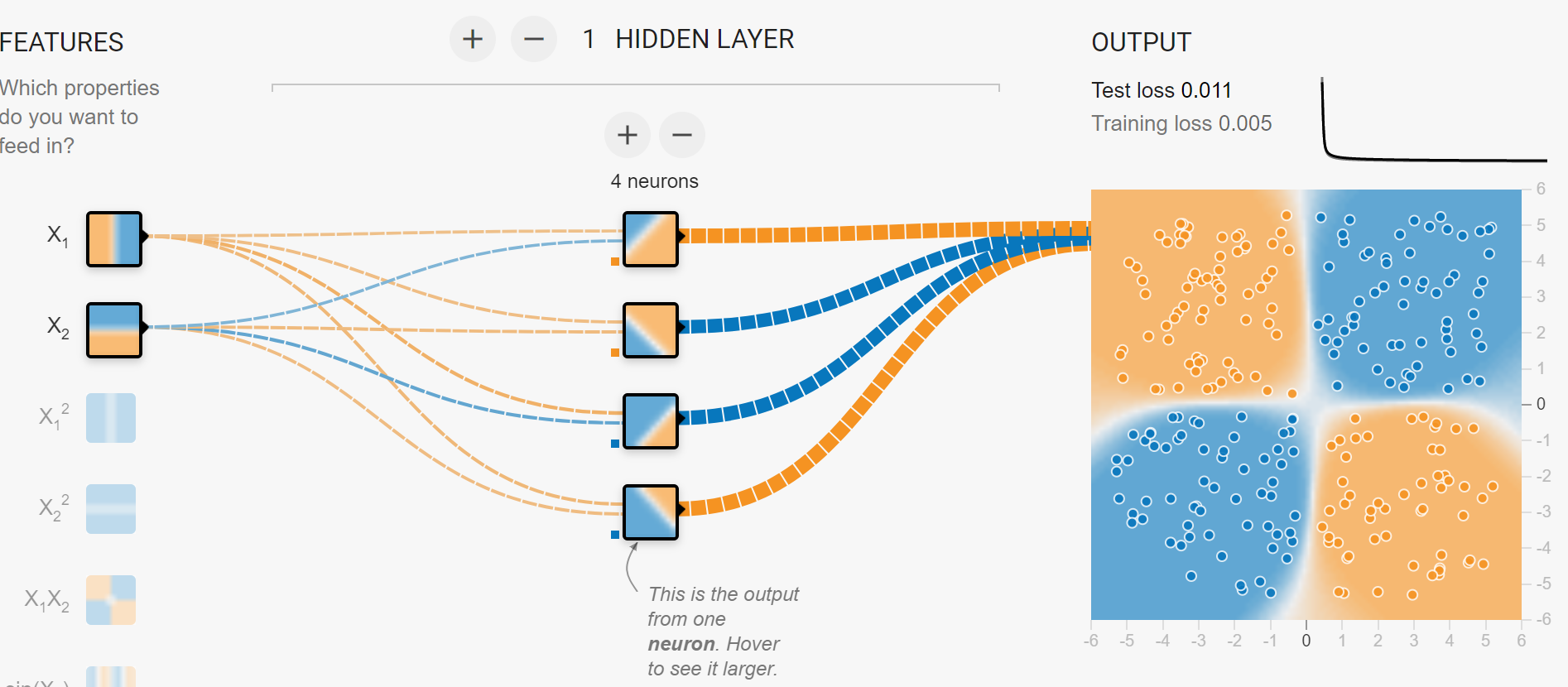
“蚊香”型双螺旋样本，需要更多的层和更多的神经元。

输出层

输出为连续变量时，最后一层的激活函数用恒等函数。

输出为分类离散变量时，最后一层输出层的激活函数 softmax 函数。要分多少类，输出层就设定多少个神经元。

训练模型：post pass

post pass: 确定最优参数的过程。

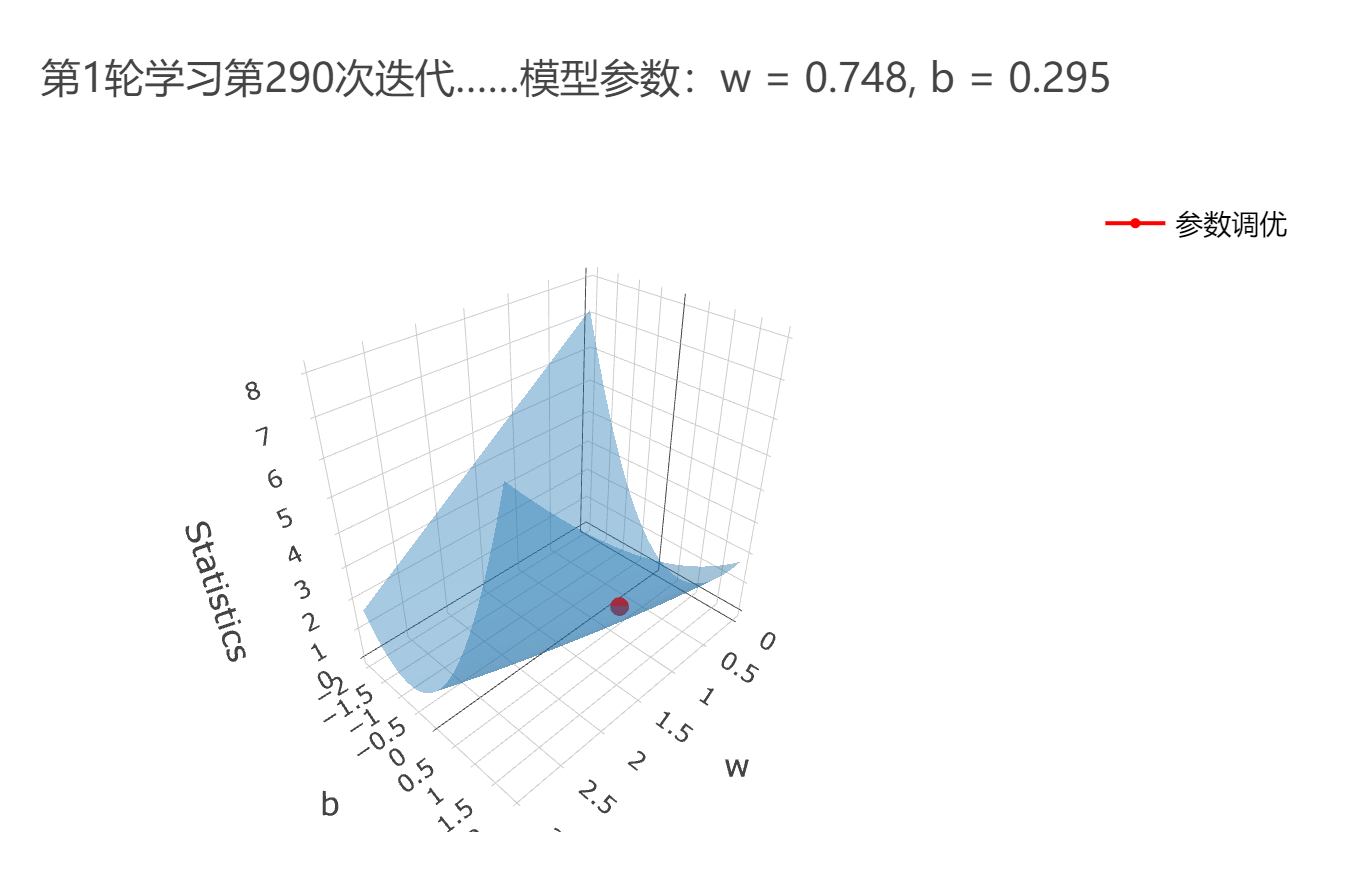
损失函数 loss function

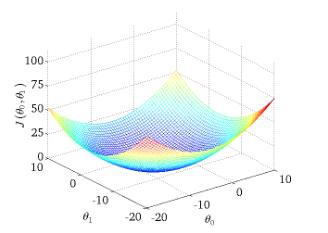
loss function: 从模型参数到模型的衡量标准统计量（比如，回归问题中常用的均方误差、分类问题中常用的交叉熵损失）的映射，表示模型性能的恶劣程度。

损失函数一般为多元函数。如图，为损失曲面（loss surface）——损失函数的可视化。

梯度下降(gradient descent)算法

寻找最佳参数束（使损失函数最小），不一定要用数学思维硬算解析解。

也可以使用计算思维：从初始参数束开始，多次迭代，每次求出损失函数的梯度，然后顺着梯度的方向小幅移动参数束。

这个过程称为“训练”或“学习”。

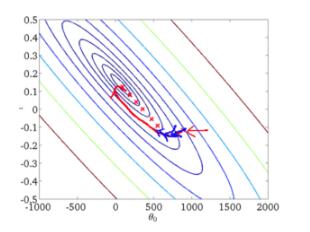
批量梯度下降（Batch Gradient Descent, BGD）

每次迭代用全部样本数据计算 loss function, 迭代结果必然向全局最优点收敛。

• 优点

  • 更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。

• 缺点

  • 当样本数目很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。

BGD 的迭代收敛曲线示意图可以表示如下：

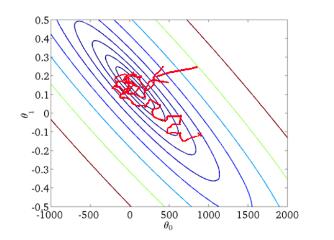
随机梯度下降（Stochastic Gradient Descent, SGD）

每次迭代时随机选取样本中的一个数据计算 loss function。

• 优点

  • 运算速度快

• 缺点

  • （1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
  • （2）可能会收敛到局部最优。
  • （3）不易于并行实现。

SGD 的迭代收敛曲线示意图可以表示如下，向全局最优点收敛的过程将是一个随机震荡的轨迹：

小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

MBGD 是对 BGD 和 SGD 的折中。其思想是：每次迭代使用一个包含部分数据的随机小样本（称为mini-batch，小批量）封装为一个张量，来计算 loss function。

批尺寸（batch size）通常设为2的n次幂（16, 32, 64, 128, 256），这样可以发挥GPU的并行计算能力。

学习率与优化器 optimizer

参数束每次迭代移动的幅度是梯度乘以学习率 $\alpha$$\alpha$，这个值可取0.03, 0.1等。

学习率是人工设定的，往往要根据训练的结果进行调整。

学习率太小，训练太慢；学习率太大，参数会在最优点附近疯狂震荡，甚至发散到无穷大。

学习率也可以是变化的，其变化策略由优化器规定：

反向传播（back propagation）算法

计算梯度要求偏导数。

如果参数数量比较大，求偏导的全局计算是非常复杂的。

因此可以用复合函数的链式求导法则，只要保存每一层的值，就可以代入链式法则算出某一点的导数。

反向传播算法使梯度下降变得可操作，从理论成为实践。

过拟合 over-fitted

正常拟合：模型在训练集和测试集上都表现良好

欠拟合：模型在训练集上的表现就不好

过拟合：模型在训练集上的表现很好，但在测试集上的表现不好。表面上，很像人类在学习中死记硬背，而没有真正地理解问题。

过拟合总是可能发生的，因此要始终监控训练集之外的数据的性能。

超参数 hyper parameter

神经网络的层数、各层神经元的数量、激活函数的形式、参数（w和b）的初始值、损失函数的形式、优化器的形式（梯度下降的具体算法）、优化器的学习率、模型训练的轮次数等，这些量属于超参数，是人为设定而模型无法训练的（一旦模型确定就不会改变）。

人们所说的调参，就是对这些超参数的人为优化设定。目前对调参尚无一套标准化的流程和方法（遍历所有超参数的计算开销过大，通常是不现实的）。

问题类型

回归问题

各输入字段的标准化，scale()

loss = "mse" 均方误差

metrics = c("mae") 平均绝对误差

数据量较少时，为避免抽样的波动，使用 K 折轮换验证

为避免过拟合太严重，使用隐藏层较少（1或2个）的小型网络

二分类问题

二分类问题中比较好的损失函数形式：loss = "binary_crossentropy"

二分类问题最后一层的激活函数应使用 sigmoid 函数，输出一个概率值。

使用时，可以对其规定阈值（可以不是 0.5！），超过该值归类为正，小于该值归类为负。

混淆矩阵

左上真正例⁵（TP），左下假正例（FP），右上假负例（FN），右下真负例（TN）

衡量指标

1. 准确率（accuracy）：(TP+TN)/(TP+TN+FP+FN). 'accuracy'也是 model.fit() 支持的度量指标。

2. 精确率（precision）：TP/(TP+FP)，即真正例/预测的正例。如果对第Ⅰ类错误不关心，可以非常保守地预测真（宁放过不错杀，提高激活函数输出正例的阈值），放宽犯第Ⅰ类错误的概率，从而提高精确率。

3. 召回率/查全率（recall 或 TPR）：TP/(TP+FN)，即真正例/实际正例。如果对第Ⅱ类错误不关心，可以非常激进地预测真（宁错杀不放过，降低激活函数输出正例的阈值），放宽犯第Ⅱ类错误的概率，而提高召回率。

4. 误报率（FPR）：FP/(FP+TN)，即误报为正的负例/实际负例。

5. ROC（receiver operating characteristic curve）曲线：在某个 epoch 轮次上，以误报率 FPR 为横轴，召回率 recall 为纵轴的曲线。

   1. 绘制这条曲线时，程序多次改变激活函数输出正例的阈值，来获得不同的分类结果。
   2. 对于每个结果，计算 FPR 和 TPR，绘制 ROC 曲线。
   3. 随着模型训练的轮次（epoch）越来越多，保持一定的 FPR，模型可以实现越来越高的 TPR. 100% 的 TPR 和 0% 的 FPR 是二分类问题的理想状态，现实中一般无法达到。

6. AUC（area under the curve），积分 ROC 曲线下方的面积，可以量化 ROC 曲线的性能，是衡量二分类模型的比较理想的指标。

二元交叉熵 binary cross entropy

这是二分类问题中比较好的损失函数形式（前述 FPR, TPR 等指标在多数点的导数为0，会使得梯度全部变为0，从而参数束无法移动）。

one-hot-encode

keras::to_categorical()，可以对分类向量进行编码，将其变为矩阵，每列为类别，符合类别赋值为1，否则为0

多分类问题

中间层神经元的个数不应小于输出层的类别数

激活函数用 softmax 函数，输出属于 n 个类别的概率分布, 每个数据点的 n 个概率值总和为1

标签使用 one-hot-encode 编码为稀疏矩阵时，损失函数用分类交叉熵 categorical cross entropy（loss = "categorical_crossentropy",）

标签为整数时，损失函数用 loss = "sparse_categorical_crossentropy"

混淆矩阵可以对模型准确度提供更细粒度的信息。

卷积神经网络

适用：空间上有关联性的数据。

MNIST 手写数字识别问题，人们把层数加得越来越深，神经元个数越来越多，还用尽了各种防止过拟合的手段，但全连接神经网络的泛化能力（模型应用于测试集的准确率）仍然不足。

卷积神经网络使用了卷积层和池化层，能够从图像输入提取有用的特征，这一架构是神经网络领域多年的研究成果。

• 卷积层的参数共享：卷积核也是反向传播训练出来的，其优点在于对图片各个区域的卷积操作共享了卷积核这一套参数
• 池化层在实践中的作用很明显，但理论上，为什么要加入池化层，几乎是未知的。

循环神经网络

适用：时间上有关联性的数据。

自然语言处理（NLP）问题。

词嵌入：根据每个词的一系列特征，将词编码为向量空间中的一个向量。

嵌入矩阵是嵌入层的参数，可以通过训练，让模型自己寻找合适的特征。

这些“特征”的含义是什么？我们不清楚。

附录：矩阵和张量运算

矩阵

矩阵求导

若 $Y=AXB$$Y=AXB$，则有 $\partial Y/\partial X=A^T{B}^T$${\partial Y}/{\partial X} = A^TB^T$

R 的张量运算

对应元素运算

sweep()对两个维度不同的张量执行扩展运算

点乘

%*%

重整 reshape

array_reshape()优先按照行排列，而 dim() <- c() 优先按照列排列，与 TensorFlow、Keras 不兼容。

因此在重整数据时，一定要用前者。

​x
1
r$> (x <- matrix(1:6, nrow = 3, byrow = TRUE))
2
     [,1] [,2]
3
[1,]    1    2
4
[2,]    3    4
5
[3,]    5    6
6

7
r$> (x_byrow <- reticulate::array_reshape(x, dim = c(6, 1)))   
8
     [,1]
9
[1,]    1
10
[2,]    2
11
[3,]    3
12
[4,]    4
13
[5,]    5
14
[6,]    6
15

16
r$> dim(x) <- c(6, 1)
17

18
r$> x
19
     [,1]
20
[1,]    1
21
[2,]    3
22
[3,]    5
23
[4,]    2
24
[5,]    4
25
[6,]    6